HighKholle | Diffusion de particules

Exercice 111 ⭐️⭐️⭐️⭐️ Membrane d’une cellule 1, ENS MP 2019, Spé/L2

Dans une cellule vivante à température ambiante, on observe une différence de potentiel de part et d’autre de la membrane qui sépare l’intérieur de la cellule, le cytoplasme, de l’extérieur. Par ailleurs, on observe une différence de concentration des ions $\displaystyle \textrm{K}{}^{+}$ comme illustré ci-dessous.

Expliquer le phénomène, sachant que la membrane est imperméable à tous les ions sauf les ions $\displaystyle \textrm{K}{}^{+}$ .
Déterminer la différence de potentiel de part et d’autre de la membrane cellulaire.

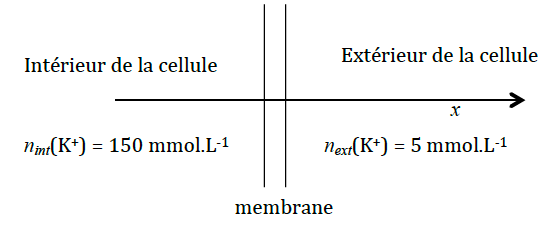
La cellule n’est évidemment pas unidimensionnelle, mais on considère ici une version simplifiée où les grandeurs étudiées ne dépendent que de $\displaystyle x$ . La membrane est schématisée ici par un double trait.

Remarque— Un énoncé plus détaillé (donc plus facile 🙂) est proposé dans l’exercice 112.
$\displaystyle k_{B}=1,38.10^{-23}\textrm{ J.K}^{-1}$ , $\displaystyle e=1,6.10^{-19}\textrm{C }$ .

Indice

Supposer un équilibre thermique, ce qui permet d’utiliser la loi de Maxwell-Boltzmann.

Corrigé

Analyse qualitative.
Considérons qu’initialement la concentration en ions $\displaystyle \textrm{K}{}^{+}$ du cytoplasme et de l’extérieur sont différentes. Alors un phénomène de diffusion de particules apparait qui tend à s’opposer à cette inhomogénéité. Donc des ions $\displaystyle \textrm{K}{}^{+}$ traversent la membrane. Comme ils sont les seuls à traverser, il va apparaitre une densité volumique de charge non nulle (négative) à l’intérieur où des charges + ont disparu, et à l’extérieur de la cellule (densité volumique de charge positive), donc un champ électrique dirigé de la région chargée positivement vers la région chargée négativement, donc de l’extérieur vers l’intérieur de la cellule.

Le champ électrique s’exerce en particulier sur les ions $\displaystyle \textrm{K}{}^{+}$ eux-mêmes. L’équilibre est atteint lorsque le courant de diffusion de particules $\displaystyle \overrightarrow{j_{P}}=-D\overrightarrow{\textrm{grad}}n$ dû à l’hétérogénéité des concentrations et le courant d’ions sous l’action du champ électrique $\displaystyle \overrightarrow{\frac{j_{e}}{e}}=n\overrightarrow{v}$ se compensent .
L’énergie potentielle d’un ion $\displaystyle \textrm{K}{}^{+}$ de charge $\displaystyle e$ dans le potentiel électrique $\displaystyle \psi$ est $\displaystyle E_{p}=e\psi$ . Ainsi la loi de Boltzmann donnant la probabilité pour un ion d’avoir une énergie potentielle $\displaystyle e\psi$ conduit à une répartition de la population des ions qui vérifie
$n\left(x\right)=n_{0}\exp\left(\frac{-e\psi\left(x\right)}{k_{B}t}\right).$

$\displaystyle n_{int}=n_{0}\exp\left(\frac{-e\psi_{int}}{k_{B}t}\right)$
et $\displaystyle n_{ext}=n_{0}\exp\left(\frac{-e\psi_{ext}}{k_{B}t}\right)$ .
D’où, avec $\displaystyle \varDelta\psi=\psi{}_{int}\text{\textendash}\psi_{ext}$ ,
$\ln\left(\frac{n_{int}}{n_{ext}}\right)=-\frac{e\Delta\psi}{k_{B}T}.$

A.N. Avec $\displaystyle T=300\textrm{ K}$ , $\displaystyle \Delta\psi=-88$ mV.

Exercice 112 ⭐️⭐️⭐️ Membrane d’une cellule 2, MP/L2

Cet énoncé reprend l’exercice 111 en précisant les étapes attendues dans la résolution.

La membrane d’une cellule vivante possède une perméabilité sélective aux ions suivant la nature des ions. À l’intérieur de la cellule (cytoplasme), les cations majoritaires sont $\displaystyle \textrm{K}{}^{+}$ . Nous considérons à présent le modèle unidimensionnel de Bernstein (1902) dans lequel seule la diffusion des ions K $\displaystyle ^{+}$ est prise en compte, la membrane étant supposée imperméable à tous les autres ions. De plus, la densité volumique des ions $\displaystyle \textrm{K}{}^{+}$ dans le cytoplasme est beaucoup plus élevée qu’à l’extérieur.
La cellule et son environnement sont en équilibre thermique à la température
$\displaystyle T$ .
Expliquer le mécanisme qui conduit à un équilibre. Justifier en particulier
l’existence d’un champ électrostatique $\displaystyle \overrightarrow{E}=E(x)\overrightarrow{u_{x}}$ , dû au déplacement des ions $\displaystyle \textrm{K}{}^{+}$ . Dans quel sens est-il dirigé à l’équilibre?
On suppose l’équilibre thermique réalisé. En déduire la différence de potentiel électrique $\displaystyle \varDelta\psi=\psi{}_{int}\text{\textendash}\psi_{ext}$ entre l’intérieur et l’extérieur de la cellule, appelée potentiel de repos. Le résultat sera exprimé notamment en fonction de $\displaystyle n_{int}$ et $\displaystyle n_{ext}$ où $\displaystyle n_{int}$ et $\displaystyle n_{ext}$ représentent les concentrations des ions $\displaystyle \textrm{K}{}^{+}$ à l’intérieur et à l’extérieur de la bactérie.
Pour la cellule étudiée à température ambiante, en déduire la
valeur numérique de son potentiel de repos $\displaystyle \Delta\psi$ .
(Question non posée dans la version ENS)
Montrer que
$\frac{1}{n}\frac{dn}{dx}=-\frac{e}{k_{B}T}\frac{d\psi}{dx},$
où $\displaystyle n(x)$ représente la densité volumique des ions $\displaystyle \textrm{K}{}^{+}$ à l’abscisse $\displaystyle x$ et $\displaystyle \psi(x)$ est le potentiel scalaire associé au champ électrostatique.
Sous l’action d’un champ électrique $\displaystyle \overrightarrow{E}$ , un ion $\displaystyle K^{+}$ dans un milieu quelconque acquiert en régime permanent une vitesse $\displaystyle \overrightarrow{v}=\mu\overrightarrow{E}$ , où $\displaystyle \mu$ est la mobilité des ions dans le milieu. Déterminer l’expression de $\displaystyle \mu$ dans la membrane en fonction du coefficient de diffusion particulaire $\displaystyle D$ dans la membrane cellulaire.

On donne la loi de Fick pour la diffusion de particules (hors programme MP) $\overrightarrow{j_{P}}=-D\overrightarrow{\textrm{grad }}n,$ où $\displaystyle \overrightarrow{j_{P}}$ est le vecteur densité de courant de particules en $\displaystyle \textrm{m}^{-2}.\textrm{s}^{-1}$ , $\displaystyle n$ est la densité particulaire, $\displaystyle D$ le coefficient de diffusion.

Réflexe

Système classique en équilibre thermique 👉 Loi de Maxwell-Boltzmann.

Corrigé

Supposons qu’initialement la concentration en ions $\displaystyle \textrm{K}{}^{+}$ du cytoplasme et de l’extérieur soient différentes. Alors un phénomène de diffusion de particules apparait qui tend à s’opposer à cette inhomogénéité. Donc des ions $\displaystyle \textrm{K}{}^{+}$ traversent la membrane. Comme ils sont les seuls à traverser, il va apparaitre une densité volumique de charge non nulle (négative) à l’intérieur où des charges + ont disparu, et à l’extérieur de la cellule (densité volumique de charge positive), donc un champ électrique dirigé de la région chargée positivement vers la région chargée négativement, donc de l’extérieur vers l’intérieur de la cellule.
Le champ électrique s’exerce en particulier sur les ions $\displaystyle \textrm{K}{}^{+}$
eux-mêmes. L’équilibre est atteint lorsque le courant de diffusion
de particules $\displaystyle \overrightarrow{j_{P}}=-D\overrightarrow{\textrm{grad}}n$ dû à l’hétérogénéité des concentrations d’une part, et le courant d’ions sous l’action du champ électrique $\displaystyle \overrightarrow{\frac{j_{e}}{e}}=n\overrightarrow{v}$ d’autre part, se compensent .
L’énergie potentielle d’un ion $\displaystyle \textrm{K}{}^{+}$ de charge $\displaystyle e$ dans le potentiel électrique $\displaystyle \psi$ est $\displaystyle E_{p}=e\psi$ . Ainsi la loi de Boltzmann donnant la probabilité pour un ion d’avoir une énergie potentielle $\displaystyle e\psi$ conduit à une répartition de la population des ions qui vérifie
$n\left(x\right)=n_{0}\exp\left(\frac{-e\psi\left(x\right)}{k_{B}t}\right).$
$\displaystyle n_{int}=n_{0}\exp\left(\frac{-e\psi_{int}}{k_{B}t}\right)$
et $\displaystyle n_{ext}=n_{0}\exp\left(\frac{-e\psi_{ext}}{k_{B}t}\right)$ .
D’où
$\ln\left(\frac{n_{int}}{n_{ext}}\right)=-\frac{e\Delta\psi}{k_{B}T}.$
A.N. $\displaystyle \Delta\psi=-88$ mV
En dérivant l’équation obtenue en 2),
$\frac{1}{n}\frac{dn}{dx}=-\frac{e}{k_{B}T}\frac{d\psi}{dx}=\frac{e}{k_{B}T}E.$
Comme vu en 1), les deux courants de particules (diffusion et électrique) se compensent :
$-D\frac{dn}{dx}+n\mu E=0.$
D’où
$\frac{\mu}{D}=\frac{e}{k_{B}T}.$