Optique géométrique
Exercice 19 ⭐️⭐️ Défaut de vision, Sup/L1
Un patient souffre d’un problème de vision. Il ne voit pas les objets nets au-delà de 26 cm, ni en-dessous de 13,5 cm .
Établir le diagnostic quant à la vision du patient : de quel défaut souffre-t-il ? Proposer une correction adaptée, tout d’abord avec une paire de lunettes qu’il portera à 2 cm de ses yeux, ensuite avec des lentilles de contact.
Avec l’âge, le patient ne pourra certainement plus lire son journal de près. Comment régler ce défaut ? Ce second problème compensera-t-il le problème initial ?
Réflexes
Modélisation de l’oeil : association d’une lentille de vergence variable (le cristallin) et d’un capteur fixe (la rétine).
Lentilles minces 👉 formules de conjugaison (Descartes ou Newton).
Corrigé
- Le patient est myope. Un oeil emmétrope (normal) peut accomoder pour faire l’image d’un objet entre et -25 cm. Ici, le cristallin correspond à une lentille trop convergente : sa distance focale maximale est plus petite que la distance fixe cristallin-rétine : l’image d’un objet à grande distance (supérieure à 26 cm) ne peut jamais se former sur la rétine.
• Pour un oeil emmétrope, lorsqu’une personne accomode, elle fait varier la courbure de son cristallin et modifie ainsi la distance focale de la lentille équivalente. varie de (sans accomodation, c’est l’observation à l’infini, c’est aussi la distance cristallin-rétine, c’est-à-dire la distance du cristallin à l’image qui est formée) à telle que
, soit .
• Pour le patient myope, varie de (lorsque l’image de l’objet à = 26 cm se forme sur la rétine, n’est pas égale à la distance cristallin-rétine) à (lorsque l’image de l’objet à = 13 cm se forme sur la rétine, n’est pas non plus égale à la distance cristallin-rétine)
et .
• La correction apportée par les lunettes doit être telle que l’image par les lunettes d’un objet situé à une distance de l’oeil entre l’infini et 26 cm se trouve à une distance en cm du cristallin . Ainsi pour un objet à l’infini, il faudrait que l’image par les lunettes soit à cm des lunettes, il faut donc une lentille divergente de focale cm ou une vergence .
On vérifie que pour un objet situé à 25 cm de l’oeil (qui correspond au P.P. de l’oeil normal), son image par les lunettes se fera à une distance d’ du cristallin telle que, numériquement, , soit =12,2 cm, soit une distance des yeux (du cristallin) de 14,2 cm.
• Pour des lentilles de contact, qu’on suppose à une position identique aux cristallins, on a directement
cm ou une vergence en dioptries.
- Avec l’âge, le patient devient presbyte, c’est-à-dire qu’il n’arrive plus à accomoder. Pour lire son journal, il lui suffit d’enlever ses lunettes et de placer le journal à 26 cm de ses yeux. En revanche, il ne verra toujours guère au-delà de 26 cm.
Exercice 49 ⭐️ Télescope de Newton, Sup/L1
Un télescope de Newton est modélisé par l’association
-d’une lentille mince , de centre optique et de distance focale .
-d’un miroir plan incliné de 45° par rapport à l’axe optique de ; l’axe optique coupe en tel que cm.
-d’une lentille mince de centre optique d’axe optique perpendiculaire à celui de , et de distance focale cm avec cm.
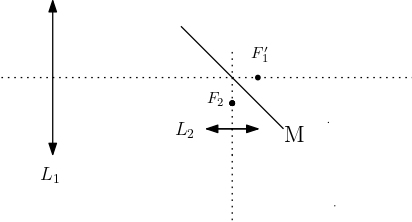
On observe Jupiter situé à une distance m et de diamètre m.
Montrer que le dispositif est afocal.
Quel est le diamètre angulaire de l’image définitive ? Commenter.
Réflexes
Dispositif afocal 👉 l’image d’un objet à l’infini est à l’infini.
Corrigé
L’image d’un objet à l’infini par la lentille convergente L1 est en . L’image par le miroir est le symétrique de par rapport à , et coïncide avec le foyer objet de la lentille , dont l’image par est à l’infini par définition.
Le diamètre angulaire de Jupiter vu de la Terre est .
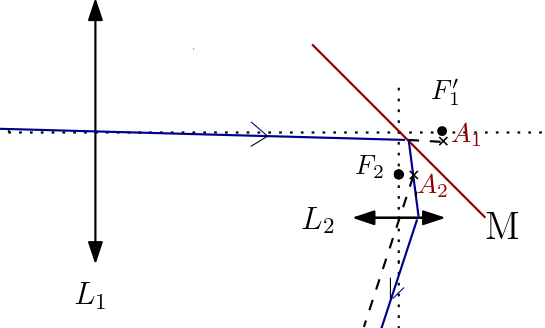
Dans le plan focal image de , l’image intermédiaire de Jupiter a un diamètre . C’est aussi le diamètre de son image par le miroir . Les rayon extrêmes du faisceau émergeant de font ainsi un angle .
A.N. Alors que est inférieur au pouvoir séparateur de l’oeil , l’image obtenue par le télescope a un diamètre angulaire radians, l’image n’apparaît pas ponctuelle.
Remarque — On peut simplifier le système en “repliant” le schéma par rapport au miroir. et se superposent, ainsi que et . On a juste une lunette afocale dont le foyer image de l’objectif est confondu avec le foyer objet de l’oculaire.
Exercice 104 ⭐️⭐️ Modélisation d’un œil, Sup/L1
Le cristallin de l’œil est assimilable à une lentille convergente de centre optique , de vergence variable . L’image se forme sur la rétine, à une distance de . L’air est d’indice et l’intérieur de l’œil est un milieu assimilable à de l’eau, d’indice . Tout se passe comme si on avait une lentille mince de vergence placée dans l’air, accolée avec un dioptre plan séparant les milieux d’indices et .
Un observateur regarde un objet , situé à 1,00 m devant ses yeux et tel que .
- Quelle est la nature de l’image (réelle, virtuelle, droite, inversée ?). Déterminer sa taille et le grandissement associé.
- Déterminer la vergence .
Réflexe
- Déterminer la vergence d’une lentille 👉 Relations de conjugaison.
- Dioptre plan 👉 Un dioptre plan est stigmatique dans l’approximation des petits angles. Un point image est le point d’intersection des rayons issus d’un point objet et déviés par la traversée du dioptre.
Corrigé
- Considérons pour simplifier que et son image sont sur l’axe optique du cristallin. Traçons le rayon issu de l’extrémité et passant par . Il est non dévié par la lentille, mais réfracté par le dioptre, puis arrive en sur la rétine.
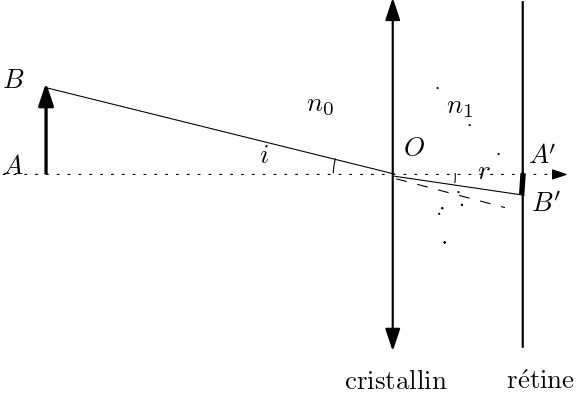
L’image se forme effectivement sur la rétine, elle est donc réelle.
Le rayon issu de passant par O, est non dévié par la lentille, mais il est dévié par le dioptre qui lui est accolé. Soient et les angles d’incidence et de réfraction correspondants. D’après Descartes, . Dans la limite des petits angles justifiée ici, et . D’où et le grandissement , l’image est inversée.
A.N. et . - Soient les images de par la lentille.
sont les images de par le dioptre.
Déterminons la position de , en utilisant l’approximation des petits angles et en considérant seulement un dioptre plan. Un rayon incident, normal au dioptre, traverse le dioptre sans être dévié. et sont donc sur la même normale au dioptre.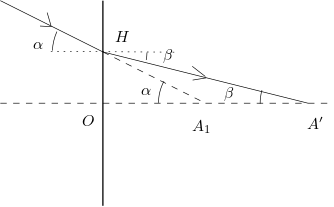
Un rayon quelconque (ou son prolongement) qui passe par arrive sur le dioptre en . Ce rayon est dévié à la traversée du dioptre et arrive en . Avec les notations de la figure,
,
d’où
Vis à vis du dioptre, est un objet virtuel.
On déduit de la position de la vergence de la lentille équivalente au cristallin avec la relation de conjugaison , soit
A.N. dioptries.
Exercice 109 ⭐️⭐️⭐️ Un mirage froid, Sup/L1
En Cornouailles, début 2021, les promeneurs ont pu observer un bateau qui semblait en lévitation au-dessus de la mer.
Pour expliquer la formation de tels mirages (mirages “froids”), on étudie la trajectoire d’un rayon lumineux dans un milieu non homogène.
- Un rayon lumineux se propage dans un milieu stratifié constitué de couches horizontales de même épaisseur, repérées chacune par un entier , et telles que l’indice de réfraction de la couche est constant. On suppose que l’indice décroit avec : pour deux entiers et si , alors . Le rayon est dans un plan vertical , et est l’angle entre le rayon qui se propage dans la couche d’indice et le vecteur unitaire horizontal .
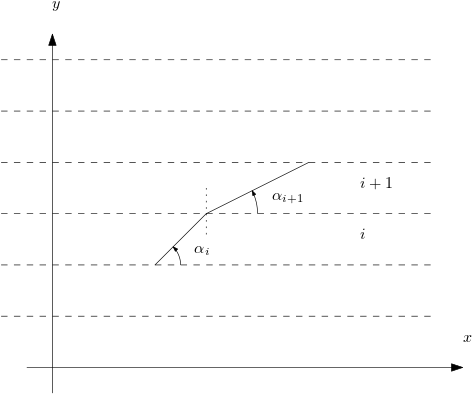
Relier les couples et .
Représenter la trajectoire d’un rayon lumineux. - On rend la stratification infiniment fine pour décrire un milieu continu. À l’ordonnée , l’indice de réfraction est et l’angle entre le rayon et est . Le point décrit la trajectoire du rayon lumineux.
- Déterminer une quantité constante en tout point de la trajectoire en fonction de et , puis exprimer en fonction de et .
- Montrer que la courbe suivie par le rayon lumineux correspond à une solution de l’équation
où on exprimera en fonction de .
- L’indice de l’air obéit à la loi de Gladstone, qui indique que est proportionnel à la masse volumique de l’air. En assimilant l’air au dessus de la mer à un gaz parfait de pression constante, préciser la dépendance de l’indice vis-à-vis de la température.
Début 2021, la température de la mer étant très basse, la température de l’air augmentait avec l’altitude à partir de la surface de l’eau. Montrer que l’étude précédente est compatible avec l’observation du mirage.
Réflexe
- Interface entre milieux d’indices différents 👉 Lois de Descartes.
- Courbe 👉 la pente de la tangente à la courbe est .
Corrigé
Les lois de Descartes indiquent que le rayon lumineux réfracté reste dans le plan vertical initial, qui est le plan d’incidence, et que .
De proche en proche, pour tout ,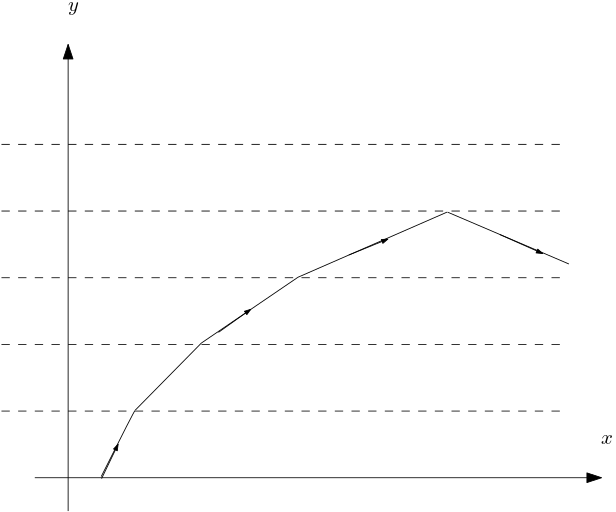
Plus augmente, plus diminue, le rayon s’écarte de plus en plus de la normale verticale. La dépendance de l’indice avec n’est pas donnée, mais il est vraisemblable qu’apparait pour une valeur de , dépendant de l’angle d’incidence initial, une réflexion totale sur l’interface .En passant à la limite continue, .
Avec , .
D’où .
En dérivant par rapport à ,
.
On calcule le second terme comme une dérivée composée . D’où .
Pour , avec .
Le cas correspond au sommet de la courbe où le rayon lumineux devient tangent à l’axe horizontal. C’est la limite de la réflexion totale. La relation reste valide par prolongement en ce point.Pour un gaz parfait, la masse volumique , masse molaire, la pression, la température. D’où
Dans l’exemple étudié, augmente quand l’altitude augmente, donc est bien une fonction décroissante de . La courbe suivie par un rayon lumineux correspond bien à une courbe telle que , de concavité tournée vers le bas.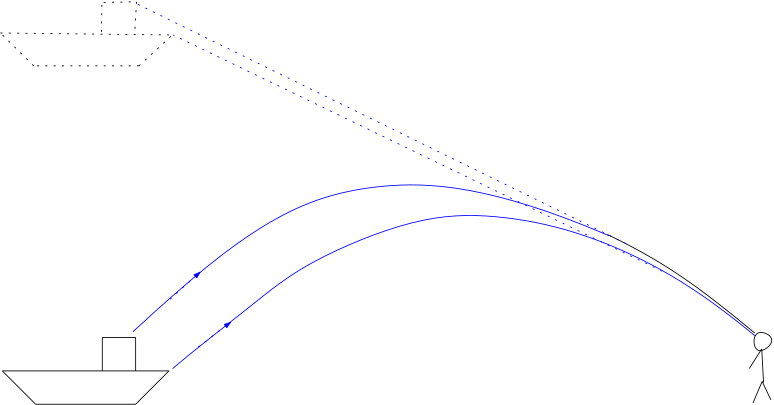
À voir, l’animation de l’université du Mans.