HighKholle | Modèle scalaire de la lumière

Exercice 73 ⭐️ Traversée d’une lame, Spé/L2

D’après Centrale TSI
Un faisceau parallèle monochromatique dans le vide arrive en incidence normale sur une lame d’épaisseur $\displaystyle e$ d’indice $\displaystyle n=1,5$ comportant un renflement d’épaisseur $\displaystyle e'$ et ressort dans le vide. Tracer la surface équiphase après traversée de la lame.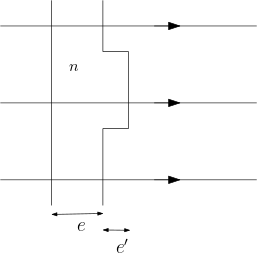

Corrigé

Écrivons l’égalité des chemins optiques parcourus pour un rayon ne passant pas par le renflement $\displaystyle (AL)$ ou passant par le renflement 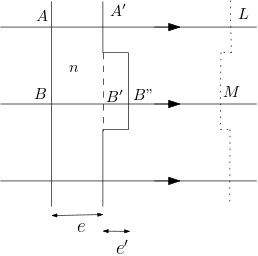$\displaystyle (BM)$ , avec $\displaystyle (AL)=(BM)$ .

$\displaystyle \left(AL\right)=ne+A'L.$

$\displaystyle \left(BM\right)=n(e+e')+B"M.$

$\displaystyle \left(AL\right)=\left(BM\right)\Rightarrow ne+A'L=n(e+e')+B"M.$

$\displaystyle \Rightarrow B'M=B"M+e'=A'L-(n-1)e'.$

Les surfaces équiphase après la lame possèdent un “creux” au niveau du renflement de largeur $e"=\left(n-1\right)e'.$

Remarque — Le théorème de Malus n’est pas mis en défaut, puisque les rayons sont bien normaux aux surfaces équiphases, mais il ne donne pas d’information permettant de trouver ces surfaces d’après les tracés de rayons.

Exercice 74 ⭐️⭐️⭐️ Modes d’une fibre optique, Spé/L2

D’après CCMP

Une fibre à saut d’indice est constituée de deux cylindres coaxiaux à section circulaire, le diamètre du cylindre intérieur (le coeur de la fibre) étant a. Le coeur est d’indice $\displaystyle n_1$ , l’espace entre les deux cylindres (la gaine) est d’indice $\displaystyle n_2$ . Pour qu’il y ait propagation dans la fibre,il faut que l’angle $\displaystyle \theta$ (voir schéma) soit inférieur à une valeur limite $\displaystyle \theta_{l}$ . Préciser cet angle et la condition sur l’angle $\displaystyle i$ correspondante.
Cette condition n’est pas suffisante : seuls certains angles d’inclinaison
conduisent à une interférence constructive et à un mode dit guidé.
Sur la figure ci-dessous, sont représentés une direction de propagation (parallèle à AB et CD) et le plan d’onde perpendiculaire $\displaystyle (\Pi)$ correspondant. La propagation dans la fibre n’est possible que si les ondes correspondant à cette direction sont en phase sur un même plan d’onde.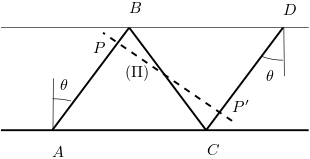

Montrer que la propagation n’est possible que pour des valeurs discrètes
de $\displaystyle \theta$ , notées $\displaystyle \theta_{m}$ où $\displaystyle m$ est un entier. Quel est le nombre de modes possibles pour une valeur $\displaystyle a=0,1$ mm , une longueur d’onde dans le vide $\displaystyle \lambda_{0}=1,5.10^{-6}$ m, $\displaystyle n_{1}=1,456$ et $\displaystyle n_{2}=1,410$ ?
Pour un mode $\displaystyle m$ donné, quelles sont les valeurs possibles de la
fréquence ? Quel type de filtrage exerce la fibre ?
Calculer la valeur maximale de $\displaystyle a$ pour avoir une fibre monomode.

Réflexes

Propagation dans la fibre 👉 Exprimer la condition de réflexion totale à l’interface coeur/gaine.
Ondes en phase 👉 Déphasage multiple de 2 $\displaystyle \pi$ , ou différence de chemin optique multiple de $\displaystyle \lambda_0$ .

Corrigé

Il doit y avoir réflexion totale à l’interface coeur/gaine, soit
$\displaystyle n_{1}\sin\theta>n_{2}$ , ou $\displaystyle \theta>\theta_{l}$ , $\theta_{l}=\arcsin\left(\frac{n_{2}}{n_{1}}\right).$
L’angle $\displaystyle r=\pi/2-\theta>\pi/2-\theta_{l}$ . Avec $\displaystyle \sin i=n_{1}\sin r$ ,
$i>\arcsin\left(n_{1}\cos\theta_{l}\right)=\arcsin\left(\sqrt{n_{1}^{2}-n_{2}^{2}}\right).$
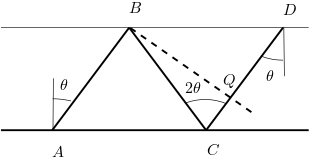
Les ondes en $\displaystyle P$ et $\displaystyle P'$ , qui appartiennent au même plan d’onde, sont en phase pour un déphasage $\displaystyle \varphi=2\pi\frac{\delta}{\lambda_0}=2m\pi,m\in\mathbb{Z}$ .
$\displaystyle \delta=n_{1}\left[PB+BC+CP'\right]=n_{1}\left[BC+CQ\right]$ .

$\displaystyle BC=\frac{a}{\cos\theta}$ et $\displaystyle BQ=BC\cos\left(2\theta\right)=\frac{a}{\cos\theta}\left(2\cos^{2}\theta-1\right)$ .
D’où $\displaystyle \delta=2n_{1}a\cos\theta$ . La condition est donc $2n_{1}a\cos\theta=m\lambda_{0},m\in\mathbb{Z}.$
La condition $\displaystyle \theta>\theta_{l}$ donne $\displaystyle \cos\theta<\cos\theta_{l}=\sqrt{1-\frac{n_{2}^{2}}{n_{1}^{2}}}$ , soit $0\leq m<\frac{2a}{\lambda_{0}}\sqrt{n_{1}^{2}-n_{2}^{2}}.$
A.N. $\displaystyle \frac{2a}{\lambda}\sqrt{n_{1}^{2}-n_{2}^{2}}=48,4.$ Il y a 49 modes possibles (de 0 à 48).
La fréquence doit vérifier $f=c/\lambda_{0}>m\frac{c}{2a\sqrt{n_{1}^{2}-n_{2}^{2}}}=f_{c,m}.$
La fibre se comporte comme un passe-haut.
Seul le mode $\displaystyle m=0$ doit pouvoir convenir. Il faut donc $\displaystyle \frac{2a}{\lambda_{0}}\sqrt{n_{1}^{2}-n_{2}^{2}}\leq1$ ,
soit $a\leq\frac{\lambda_{0}}{2\sqrt{n_{1}^{2}-n_{2}^{2}}}.$
A.N. $\displaystyle a\leq2,0\textrm{ }\mu\textrm{m}$ . Dans ce cas, $\displaystyle \theta=\pi/2$ , la propagation se fait selon l’axe de la fibre.

Exercice 75 ⭐️⭐️ Lois de Descartes, Spé/L2/Classique

Un faisceau lumineux parallèle se propageant dans un milieu d’indice $\displaystyle n_{1}$ arrive avec un angle d’incidence $\displaystyle i_{1}$ sur une interface plane avec un milieu d’indice $\displaystyle n_{2}$ . Le faisceau parallèle transmis fait un angle $\displaystyle i_{2}$ avec la normale à l’interface. On admet la première loi de Descartes : les rayons réfléchis et transmis sont dans le plan d’incidence (formé par un rayon incident et la normale au point d’intersection du rayon avec l’interface).

En utilisant le théorème de Malus, démontrer la loi de Descartes pour
la réfraction.

Faire un raisonnement analogue pour la loi de la réflexion.

Corrigé

Théorème de Malus : les rayons lumineux sont normaux aux surfaces
d’onde ou surfaces équiphases.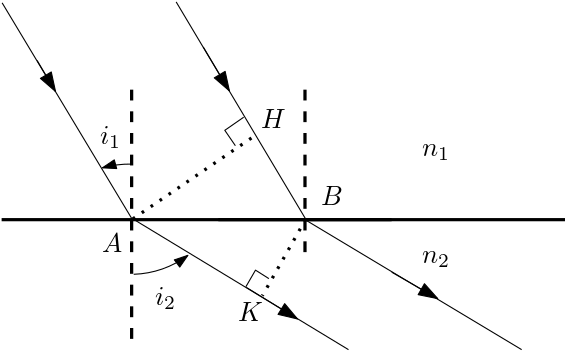

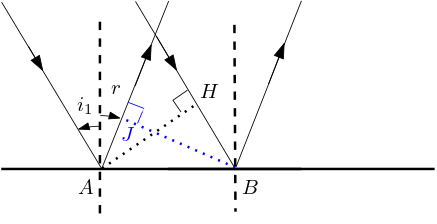
Les deux ondes se propageant selon les rayons passant par $\displaystyle A$ et $\displaystyle B$ sont en phase d’une part en $\displaystyle A$ et $\displaystyle H$ , d’autre part en $\displaystyle B$ et $\displaystyle K$ . Donc $\displaystyle \left(AK\right)=\left(HB\right)$ , soit $\displaystyle n_{2}AK=n_{1}HB\Longleftrightarrow n_{2}AB\sin i_{2}=n_{1}AB\sin i_{1}$ .

$n_{1}\sin i_{1}=n_{2}\sin i_{2}.$

Dans le cas de la réflexion , on obtient de même $\displaystyle \left(AJ\right)=\left(HB\right)$ , soit $r=-i$ .