Interférences à N>2 ondes
Exercice 40 ⭐️⭐️ Interférences à 3 ondes, classique, Spé hors PSI/L2
Trois fentes très fines identiques parallèles à sont situées dans le plan en . Ces trois fentes sont éclairées en incidence normale par une source monochromatique de longueur d’onde . Les interférences sont observées à l’infini sur un écran parallèle au plan des fentes placé dans le plan focal image d’une lentille convergente de distance focale . L’ensemble se trouve dans l’air assimilé au vide. Exprimer l’éclairement obtenu en un point de l’écran.
Réflexes
- Interférences à n>2 ondes 👉 Sommer les amplitudes complexes.
- Interférences à l’infini 👉 Evaluer le déphasage avec la loi du retour inverse + théorème de Malus.
Corrigé
Pour un point M de l’écran, appelons l’amplitude complexe de l’onde issue de la fente (en ) telle que .
L’amplitude complexe de l’onde issue de la fente du milieu est où .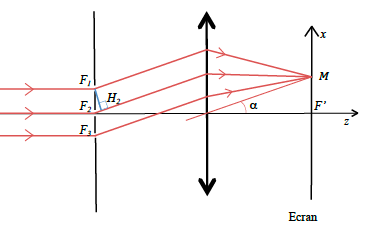
.
En utilisant le principe de Malus et la loi du retour inverse de la lumière
, et dans l’approximation de Gauss.
De même .
Les ondes issues des 3 fentes sont cohérentes, l’amplitude complexe résultante en M
L’éclairement avec facteur de proportionnalité, soit
étant l’éclairement obtenu quand une seule fente est ouverte.
L’éclairement, fonction de , est périodique, et pair, avec sur un maximum absolu pour (toutes les ondes sont en phase) et un maximum relatif pour (les ondes 1 et 3 sont en phase, l’onde 2 en opposition de phase). Le minimum d’éclairement nul est obtenu pour .
En fonction de la position de M,
On observe ainsi sur l’écran des franges rectilignes parallèles à , avec des franges très brillantes séparées de . Partant d’une frange brillante, on observe à une distance une frange sombre, puis à une frange brillante d’intensité 9 fois plus faible, et à une nouvelle frange sombre.
Exercice 61 ⭐️⭐️⭐️ Réseau en escalier, Spé hors PSI/L2
On considère marches d’escalier (largeur a et hauteur b de l’ordre du m pour chaque marche) placées dans l’air assimilé au vide. Au milieu de chaque marche, il y a un miroir très fin parallèle aux marches. Une onde monochromatique de longueur d’onde éclaire toutes les marches en incidence normale.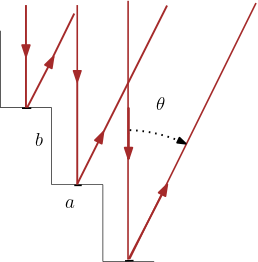
Pour quelle valeur de a-t-on un maximum d’intensité ? Quel est l’intérêt de ce dispositif par rapport à un réseau par transmission usuel ?
(MP) Calculer pour un angle donné l’intensité diffractée à l’infini et la représenter graphiquement.
Réflexes
- Maximum d’intensité 👉 Les ondes sont en phase.
- Calcul de l’intensité (ou éclairement) pour N>2 ondes 👉 Sommer les amplitudes complexes pour obtenir l’amplitude résultantes avant de passer à l’intensité.
Corrigé
- Il s’agit d’un réseau par réflexion. Les miroirs étant “très fins”, la diffraction par un miroir se fait dans tout le demi-espace disponible, et le problème se ramène à l’interférence des ondes dans la direction .
Evaluons la différence de marche entre les rayons se réfléchissant sur deux marches consécutives.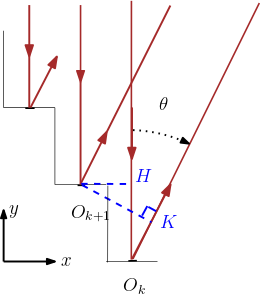
avec , et .
Les maxima d’intensité correspondent à .
Soit .
(avec pour que les rayons puissent émerger.
L’intérêt d’un tel dispositif est que les maxima sont obtenus pour des ordres élevés, ce qui permet d’obtenir un meilleur pouvoir de résolution : pour un faible écart de longueur d’onde, l’écart angulaire vérifie
- Soit l’amplitude complexe diffractée par la marche n°1 dans la direction d’angle , et soit le déphasage entre les ondes issues de deux fentes consécutives. L’amplitude résultante est
Avec ,
Les maxima principaux sont bien obtenus pour , soit .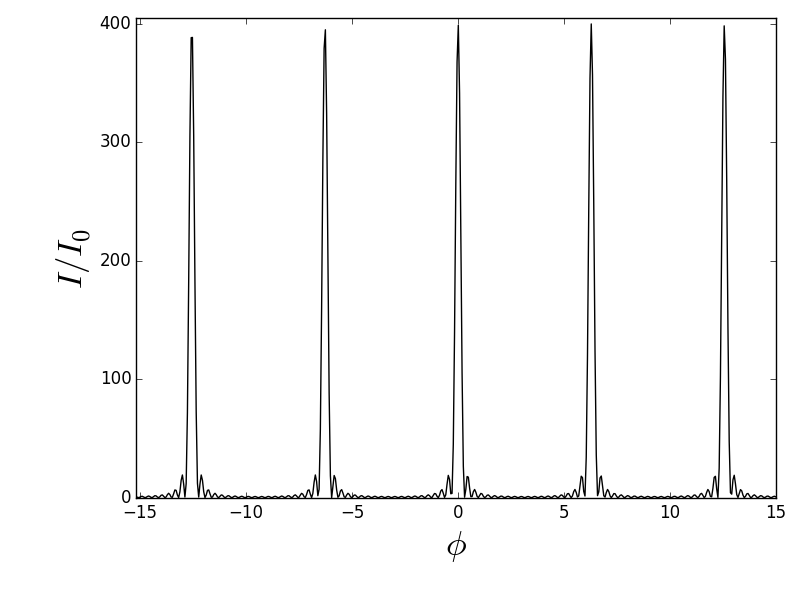
(pour 20 fentes)
Exercice 124 ⭐️⭐️⭐️ Réseau blazé, Centrale MP 2021, Spé hors PSI/L2
Le spectrographe Elodie comporte un réseau “blazé”, constitué de facettes réfléchissantes parallèles disposées périodiquement comme indiqué sur le schéma, dont l’objectif est de disperser les rayons qu’il reçoit.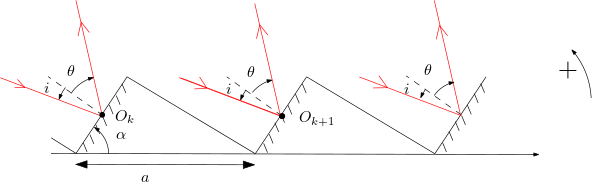
Comme les facettes sont très fines, la lumière diffractée n’obéit pas aux lois de Descartes (c’est comme la diffraction par une fente très fine, la lumière est renvoyée dans toute une région de l’espace). Un détecteur est placé à l’infini (dans le plan focal d’une lentille convergente) dans la direction faisant un angle avec la normale aux facettes.
Les rayons incidents viennent d’une source ponctuelle monochromatique de longueur d’onde , située à l’infini dans la direction faisant un angle avec la normale aux facettes.
Justifier que les deux ondes associées aux rayons se réfléchissant en et peuvent interférer.
Montrer que le déphasage entre ces deux ondes estLa source est maintenant polychromatique, , avec une incidence normale .
a) Déterminer l’ordre d’interférence pour , et le comparer à celui d’un réseau par transmission usuel, dont l’écart entre deux fentes est .
b) Donner les valeurs et sachant que avec ,.La source comporte un doublet de longueurs d’onde et , l’incidence est normale .
a) Du fait de l’effet Doppler-Fizeau, pour une longueur d’onde émise par une étoile, un observateur mesure une valeur où est la vitesse radiale de l’étoile (selon l’axe Terre-Étoile) et la vitesse de la lumière. Exprimer en fonction de , de la variation de la vitesse de l’étoile sur sa trajectoire et de .
b) L’étoile possède une exoplanète qui crèe une variation de la vitesse radiale de l’étoile. Pour caractériser l’exoplanète, on veut pouvoir distinguer la variation de vitesse radiale lorsque cette vitesse passe de 14,68 km.s à 14,85 km.s. L’observation est faite dans l’ordre pour la longueur d’onde nm. Déterminer l’expression de la variation de l’angle à la sortie du réseau associée à la variation observée. Calculer numériquement la valeur de . Commenter.
Réflexe
Source à l’infini et observation à l’infini 👉 utiliser les plans équiphases perpendiculaires aux rayons pour évaluer les déphasages.
Corrigé
Les deux ondes sont issues de la même source et sont synchrones, cohérentes (leur déphasage, comme explicité ensuite, ne dépend pas du temps), elles interférent donc.
On s’intéresse au déphasage entre deux ondes de directions repérées par et , il s’agit d’interférences à l’infini. étant la source, . De même, étant le point d’observation à l’infini .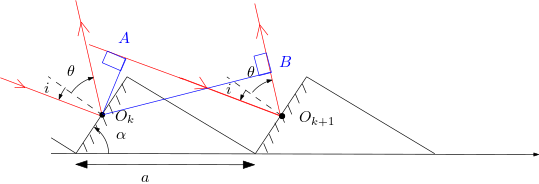
Le déphasage entre les deux ondes est donc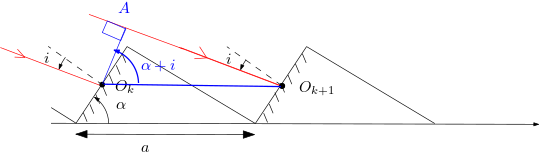
De même, avec sur le schéma,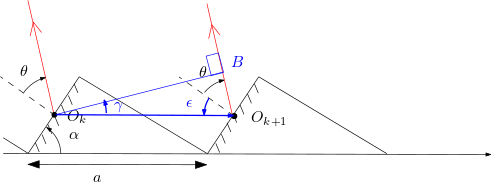
D’où .
Remarque — Le résultat se retrouve en remarquant qu’on cherche la somme des déphasages en par rapport à pour les ondes planes incidente et émergente. En appelant l’axe , les vecteurs d’onde des ondes planes sont
et
,
redonne le même résultat.a) Pour , , donc
, alors que pour un réseau par transmission usuel .
b)
et .
3.a) .
b)
.
En différentiant,
.
A.N.,
Ce réseau permet de travailler dans des ordres élevés, et d’avoir une meilleure résolution par rapport à un réseau classique où reste de l’ordre de quelques unités. Ici, cela permet de déterminer précisément la variation de vitesse .
Exercice 165 ⭐️⭐️⭐️ Interférences à trois ondes, CCMP MP2023, Spé hors PSI
On étudie l’intensité produite sur un écran par le dispositif suivant :
-source au foyer objet d’une première lentille convergente,
-observation dans le plan focal image d’une seconde lentille convergente,
-entre les deux lentilles un écran percé de trois trous identiques distants de ,
-devant l’écran percé de trous, une lame de verre d’indice avec un renflement d’épaisseur .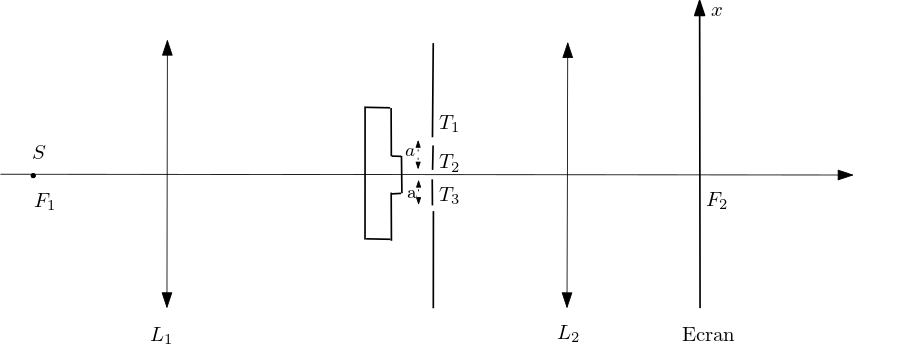
La source est ponctuelle et monochromatique de longueur d’onde . On observe une répartition de l’intensité suivant la courbe noire sans la lame de verre et suivant la courbe rouge avec la lame pour une épaisseur e donnée.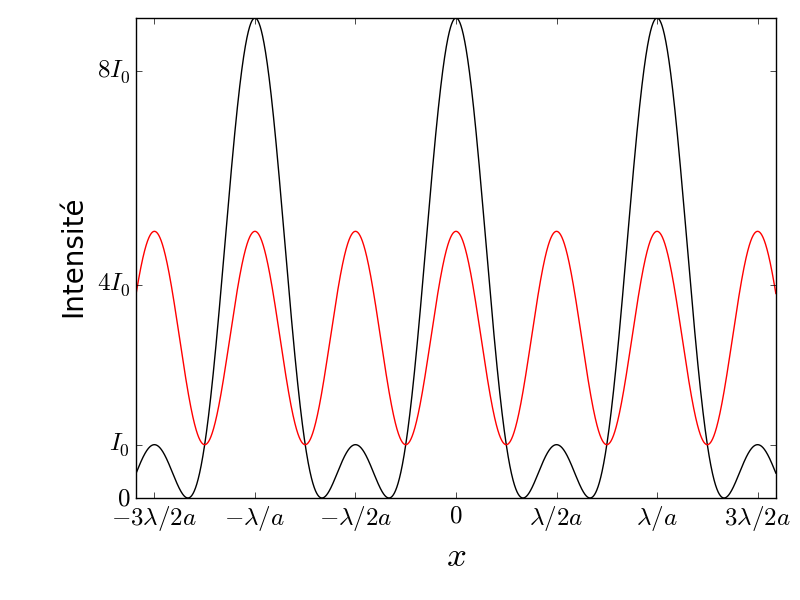
- Déterminer l’intensité si l’on enlève la lame, puis avec la lame pour quelconque.
- Donner l’épaisseur minimale pour obtenir la courbe rouge.
- On obstrue la fente du milieu, donner .
Réflexes
Interférences à ondes multiples 👉 Utiliser les amplitudes complexes.
Corrigé
Sans la lame
En utilisant les amplitudes complexes des ondes passant par les trois trous, l’amplitude résultante en un point de l’écran repéré par sa coordonnée est (avec la convention )
,
où le déphasage s’exprime classiquement en fonction de la différence de marche entre deux ondes voisines , sous la forme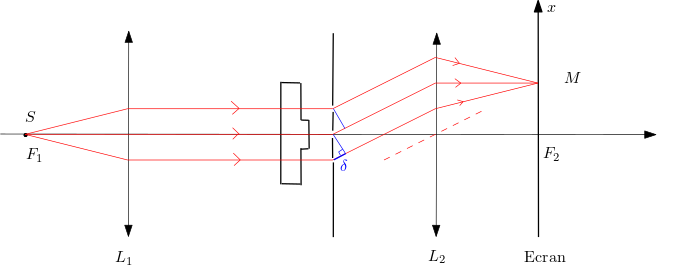
D’où l’intensité
où est l’intensité en quand un seul trou est présent.
L’intensité est une fonction paire de , de période . Une étude des variations sur montre deux maxima en 0 et , et un minimum en , conformément à la courbe noire donnée.
Avec la lame
L’onde du milieu parcourt un chemin optique supplémentaire par rapport aux autres
où . L’intensité devient
.La courbe rouge présente une période . Il faut donc que le terme en soit annulé par ,
soit
entier. La plus petite valeur de qui convient est
Dans ce cas, , correspondant à la courbe rouge, périodique, de valeur moyenne . Le déphasage imposé supplémentaire de pour le trou du milieu permet à l’intensité de ne jamais s’annuler.Dans ce cas, on retrouve les trous d’Young distants de , le trou du milieu ayant disparu :
L’intensité devient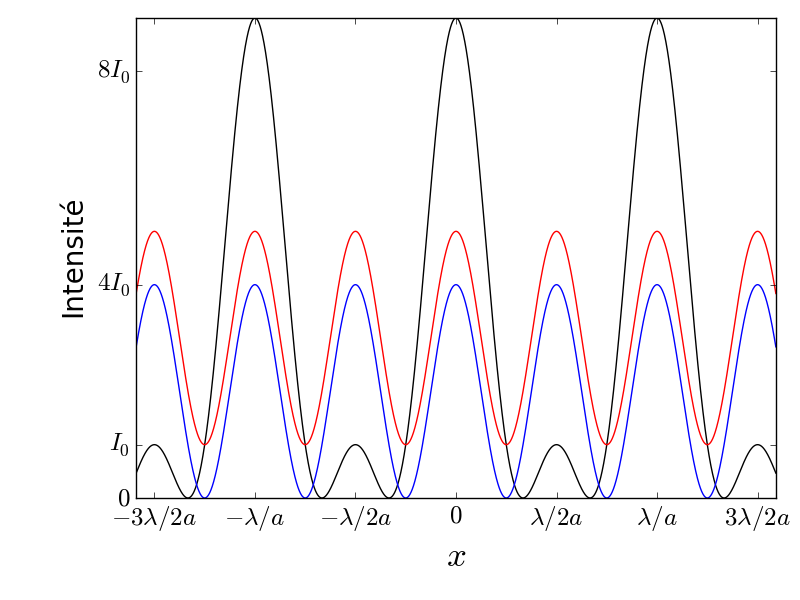
L’intensité (en bleu) est périodique comme dans le cas de la courbe rouge, mais les minima sont nuls.