Ondes mécaniques
Exercice 10 ⭐️⭐️⭐️ Onde dans un cristal, X MP 2018, Spé/L2
Un cristal est modélisé par un réseau d’atomes de masse liés les uns aux autres par des liaisons assimilables à des ressorts. La masse est liée à la masse et par un ressort de raideur , et elle est liée aux masses et par un ressort de raideur . A l’équilibre, deux atomes consécutifs sont distants d’une longueur , de telle sorte que l’abscisse de l’atome est . Lors d’une excitation, l’abscisse de l’atome est .
Trouver l’équation de dispersion des ondes dans ce milieu, puis étudier les cas particuliers. Que se passe-t-il si on excite avec une pulsation trop grande ?
Réflexe
Equation de dispersion 👉 Etablir une équation de propagation et y injecter une représentation complexe du signal.
Indice
Indice : chercher l’onde sous la forme .
Corrigé
Faisons un bilan des forces exercées sur l’atome
• ressort lié à l’atome : .
• ressort lié à l’atome : .
• ressort lié à l’atome : .
ressort lié à l’atome :
En référentiel supposé galiléen, le principe fondamental de la dynamique projeté sur donne :
.
Supposons qu’il existe une onde associée à ces déplacements de telle sorte que . D’où :
.
Avec et ,
.
• La limite correspond à la limite des grandes longueurs d’onde , d’où l’approximation continue est valide (on pourrait la retrouver en faisant des dl à l’ordre 2 de et où ).
. Dans ce cas on trouve une propagation non dispersive de vitesse de phase .
• En dehors de cette limite la propagation est dispersive car est non constant.
• La valeur maximale possible de est . Pour une pulsation plus grande, il n’y a pas propagation.
Exercice 20 ⭐️⭐️⭐️ Corde avec force de Laplace, Spé/L2
Une corde de longueur , de masse linéique , de poids négligeable, est tendue sous une tension . Elle est confondue au repos avec l’axe horizontal. Elle est parcourue par un courant permanent et placée dans un champ magnétique . Sous l’effet d’une excitation sinusoïdale, elle subit des petites déformations et .
Rappeler l’équation de propagation des petites déformations d’une corde vibrante tendue, la corde restant dans un plan vertical.
Exprimer la force de Laplace exercée sur un élément de corde compris entre et en fonction de et , et déterminer les équations différentielles couplées vérifiées par les fonctions et .
On cherche et sous la forme et . Chercher la relation de dispersion et interprétez.
Réflexes
Équation de dispersion 👉 Insérer les représentations complexes dans les équations de propagation.
Corrigé
avec .
La force de Laplace est
En référentiel terrestre supposé galiléen, considérons le système : élément de corde comprise au repos entre et .
Actions exercées : les tensions et .
Appliquons la relation fondamentale de la dynamique :
. On projette sur
. Avec ,
- sur : de même,
Pour qu’il y ait des solutions non nulles, il faut que le déterminant du système de deux équations à deux inconnues soit nul :
,
soit ou
La résolution des deux équations conduit à des valeurs réelles de : il y a propagation sans amortissement ni amplification.
En remplaçant dans une des équations,en et , on voit que . La corde “tourne” dans un sens ou dans l’autre, on peut signaler l’analogie avec une OPPH électromagnétique de polarisation circulaire ou elliptique.
Exercice 45 ⭐️⭐️⭐️ Chaîne chargée, Spé/L2
On s’intéresse à une chaîne unidimensionnelle infinie de charges ponctuelles de même masse , de charges alternativement égales à et , qui se trouvent au repos régulièrement réparties sur l’axe , chaque charge se trouvant à une distance de ses voisines. Sous l’action d’une perturbation, les charges se déplacent sans frottements selon une direction perpendiculaire à l’axe de la chaîne. On néglige toute influence de la pesanteur, et on suppose que l’amplitude des déplacements est faible devant .
La charge est ainsi repérée par ses coordonnées et . On cherche à étudier la propagation d’ondes relatives au déplacement .
Etudier le cas où l’on ne tient compte que des interactions entre proches voisines. Quelle est la pulsation maximale des oscillations ? Exprimer la vitesse de propagation dans la limite non dispersive.
On tient compte maintenant des interactions entre toutes les charges.
Que devient la relation de dispersion dans la limite où ?
On admettra que .
Réflexes
Limite non dispersive 👉 Relation linéaire entre et .
Indice
Onde sur une chaîne discrète 👉 Chercher l’onde sous la forme
.
Corrigé
- La charge repérée par sa position est soumise aux forces
exercées par ses plus proches voisines :
et .
.
.
En référentiel supposé galiléen, on applique le principe fondamental de la dynamique à la charge en projection sur
En se limitant à un développement au premier ordre non nul en ,
, soit
On retrouve l’équation usuelle d’une chaîne d’oscillateurs.
• On cherche une onde de la forme . En remplaçant dans (1) :
, soit la relation de dispersion
La pulsation maximale est
.
• Une propagation non dispersive correspond à une relation de dispersion de la forme . Cela correspond à la limite , c’est-à-dire à l’approximation des milieux continus.
En se plaçant directement dans ce cas, avec telle que
,
et
D’où
On reconnait une équation de d’Alembert de célérité dont on vérifie l’homogénéité en pensant à la force coulombienne .
- La force exercée par la charge sur la charge est
.
La force exercée par la charge sur la charge est
Le principe fondamental de la dynamique à la charge en projection sur donne ainsi
On cherche encore une onde de la forme .
,
soit .
Suivant l’énoncé, on en déduit dans la limite des milieux continus, tels que ou ,
, soit
La célérité est dans ce cas
Exercice 83 ⭐️ Relation de dispersion en eau profonde, Spé/L2
Pour la propagation des ondes à la surface de l’eau dans le cas de grandes profondeurs, la vitesse de phase et la vitesse de groupe vérifient Que peut-on dire de la relation de dispersion?
Exprimer la relation de dispersion par analyse dimensionnelle en faisant apparaître le champ de pesanteur g, avec un coefficient de
proportionnalité égal à 1. En déduire l’expression de en fonction de la la fréquence.
Corrigé
Par séparation des variables, .
En intégrant, où est une constante d’intégration.
D’où où est une constante de dimension .
Avec un coefficient de proportionnalité égal à 1, la relation de dispersion est
En fonction de la fréquence
Exercice 84 ⭐️⭐️ Cône Tcherenkov, Sup/L1
D’après X PC 2019
Une particule chargée est en mouvement rectiligne uniforme à la
vitesse . Elle émet en chaque point de sa trajectoire une onde sphérique se propageant à la vitesse , qu’on suppose constante. Montrez que
si , les points de l’espace atteints par l’onde occupent l’intérieur
d’un cône dont vous préciserez l’axe et le demi-angle au sommet, et que vous représenterez sur un schéma.Dans les détecteurs de neutrinos comme Super-Kamiokande au Japon,
les neutrinos sont détectés quand ils rentrent en collision avec des molécules d’eau. Un électron, de vitesse voisine de , est alors éjecté et émet un rayonnement électromagnétique (rayonnement Tcherenkov). L’indice de l’eau est . Quel est l’angle entre la direction de l’électron et le rayonnement Tcherenkov ?
Corrigé
Soit la position de la particule à la date . L’onde émiseà depuis la position telle que , atteint à la sphère de rayon centrée sur . Cette onde se trouve ainsi à à l’intérieur d’un cône d’angle tel que
, indépendant de .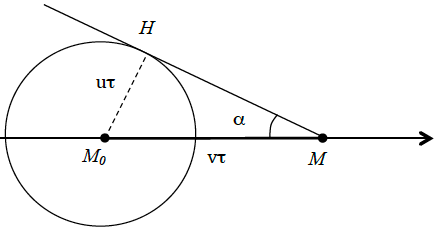
Ainsi, les points de l’espace atteints par l’onde occupent l’intérieur d’un cône dont l’axe est donné par la trajectoire de la particule, et de demi-angle au sommet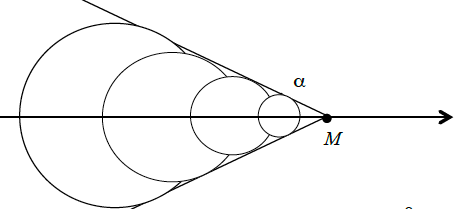
- Ici et . D’où .
Remarque — Un autre exemple est le cône de Mach observé dans le cas
d’un avion supersonique.
Exercice 85 ⭐️⭐️⭐️ Sillage d’un canard, Sup/L1
Un canard se déplace rectilignement sur un lac à la vitesse uniforme . Son passage provoque l’émission d’ondes, sous forme de vaguelettes, à la surface de l’eau dans toutes les directions.
Pour une onde se propageant dans la direction qui fait un angle avec la direction de déplacement du canard, l’énergie de l’onde, dont dépend le sillage, se déplace à la vitesse .
En déduire l’angle du sillage d’un canard. Qu’en est-il d’un paquebot ?
Remarque pour les curieux (niveau Spé) — La vitesse de propagation d’une onde de longueur d’onde donnée ne dépend pas de la direction d’émission, mais selon l’analyse de Kelvin, seules sont observées les ondes stationnaires de longueur d’onde telle que la vitesse de l’eau dans le référentiel du bateau projetée sur la direction de propagation de l’onde s’oppose exactement à la vitesse de phase de l’onde, soit . Avec la relation valable pour les ondes de surface en eau profonde, on obtient la relation donnée.
Rappel — L’équation en coordonnées polaires d’un cercle de diamètre , passant par l’origine et par le point situé sur l’axe polaire d’abscisse est .
Indice
Représenter sur un schéma la position du canard à la date , la position du canard à la date , et le lieu des points atteints à la date par l’onde émise par le canard à la date .
Corrigé
L’onde émise à dans la direction a parcouru à la date la distance . Le lieu des points atteints par l’onde est donc le cercle de diamètre .
Ce cercle passe par le milieu des positions et du canard à et . Les points du cercle sont tous contenus dans le cône de sommet et d’angle , tel que
indépendant de et .
On peut remarquer que toutes les ondes sont émises vers l’avant dans le référentiel terrestre : pour . Par exemple, pour une émission dans la direction , d’où .
Ainsi à la date , toutes les vaguelettes créées par le passage du canard sont comprises dans un cône d’angle °, qui définit le sillage du canard.
La résolution est identique pour les paquebots !
Remarques
— Il est intéressant de comparer ce résultat à celui de l’exercice 84, en milieu non dispersif, sur le cône Tcherenkov, ou cône de Mach, dans lequel l’angle du “sillage” est .
— La relation donnant la vitesse des ondes doit être modifiée quand augmente ; le sillage d’un bateau rapide de type « cigarette » est plus étroit.
Pour les curieux, un bel article de “Reflets de la physique” sur le sujet se trouve ici.
Exercice 90 ⭐️⭐️⭐️ Chaîne de cellules RC, Spé/L2
D’après Centrale.
Une ligne infinie est constituée de cellules, associant chacune une résistance et un condensateur de capacité . Cette ligne est alimentée par un générateur idéal de tension sinusoïdale de f.é.m . En régime sinusoïdal forcé (RSF), la tension aux bornes du condensateur est , de représentation complexe .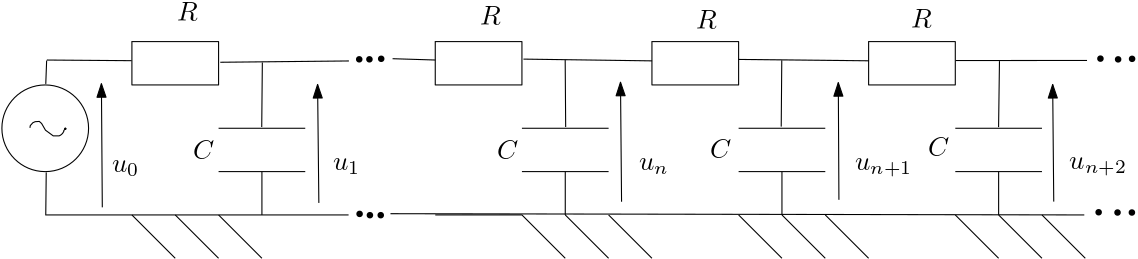
Etablir la relation de récurrence liant les .
On cherche une solution de la forme .
Montrer que c’est possible si vérifie une condition à expliciter.Dans la suite, . Montrer que
au second ordre près en .
Interpréter le caractère complexe de . Déterminer au même ordre d’approximation que . Lever l’indétermination de signe sur .
.Comme , est proche de l’unité. Montrer que l’amplitude de présente une décroissance quasi exponentielle du type . Exprimer .
Combien de cellules faut-il pour avoir une atténuation de l’amplitude
supérieure à 99% ?Les condensateurs sont repérés par leur position où est la taille d’une cellule. La fonction de deux variables est définie telle que . On suppose que la variation spatiale de la fonction est faible sur une échelle de distance de l’ordre de . Montrer que vérifie une équation différentielle de la forme
Réflexe
La fonction de deux variables est définie telle que 👉 Approximation des milieux continus.
Corrigé
Soit . Avec la loi des noeuds ,
d’où
En RSF avec la représentation complexe : .,
soit ..
Avec , ,
complexe décrit un déphasage entre deux tensions successives et .
.
En ne gardant que les premiers termes du développement,
Il ne peut y avoir qu’atténuation car les composants en jeu sont des
dipôles passifs, donc . Donc ., .
Par identification avec ,
, soit
Pour , .Il s’agit de l’aproximation des milieux continus :
En remplaçant dans l’équation du 1), avec en m.s. On obtient ainsi une équation de diffusion. Une telle équation peut être ainsi simulée expérimentalement par une chaîne de cellules .
Exercice 132 ⭐️⭐️⭐️ Modélisation discrète de propagation du son , Spé/L2
Afin de modéliser la propagation du son dans une conduite cylindrique horizontale, on considère un grand nombre de cellules remplies d’un gaz parfait de coefficient , séparées par des cloisons d’aire S, d’épaisseur négligeable et de masse surfacique Au repos la cloison se trouve dans le plan d’abscisse et à la date , elle se trouve dans le plan d’abscisse Au repos, le gaz dans chaque cellule occupe un volume sa pression est . A l’instant le volume de la cellule entre et est sa pression est .
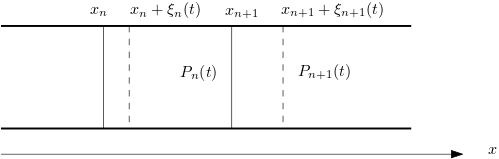
On considère que l’évolution du gaz dans chaque cellule est isentropique et que pour tout , .
Déterminer la relation entre
Déterminer la relation entre .
En déduire la relation entre
Préciser l’approximation des milieux continus. En déduire l’équation vérifiée par la fonction telle que . Quelle est la solution générale de cette équation?
On se place dans la situation où l’approximation des milieux continus n’est pas possible. On étudie une solution de la forme .
Pourquoi suffit-il de faire varier entre et ? Déterminer la relation de dispersion, la vitesse de phase, la vitesse de groupe. En donner la représentation graphique. Quelle est la nature de ce filtre ?
Réflexes
- Evolution isentropique d’un gaz parfait 👉 Loi de Laplace.
- Approximation des milieux continus 👉 Interpoler la fonction discrète de l’espace par une fonction continue lentement variable sur une distance caractéristique de d.
Corrigé
En référentiel terrestre supposé galiléen, la cloison est soumise à deux forces horizontales de pression exercées par les compartiments de gauche et de droite .
La seconde loi de Newton projetée sur donne, en
divisant par ,L’évolution du gaz parfait étant isentropique, la loi de Laplace s’applique , soit, .
Avec ,En injectant dans l’équation du 1),
L’approximation des milieux continus consiste à construire une fonction , telle que , interpolation de , et de considérer petit devant la distance caractéristique d’évolution de . Alors et au second ordre en ,
.
D’où
On obtient une équation de d’Alembert, associée à une propagation non dispersive de célérité .
Avec en kg.m, d en m et en kg.m.s, est bien homogène à une vitesse.
La solution générale est de la forme .Pour tout entier, est
périodique en , ce qui justifie le domaine d’étude de .
En injectant les expressions des dans l’équation de propagation, on obtient
,
soit la relation de dispersion
ou La fonction est paire, la valeur >0 ou <0 de correspondant aux deux sens de propagation possibles.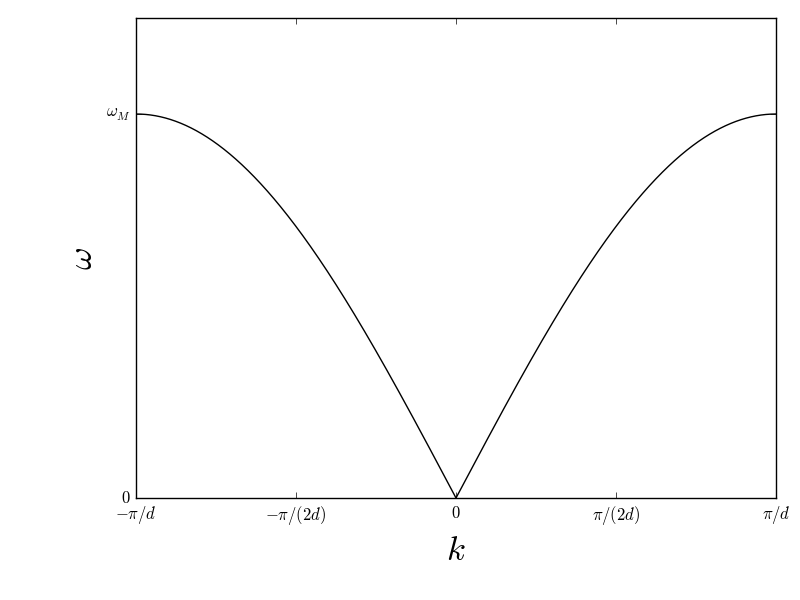
Remarque — Pour , on retrouve la limite des milieux continus et la propagation non dispersive.
La vitesse de phase (entrait plein sur la figure), par exemple pour , est
De même la vitesse de groupe (en tirets sur la figure) On constate q’uelle s’annule pour .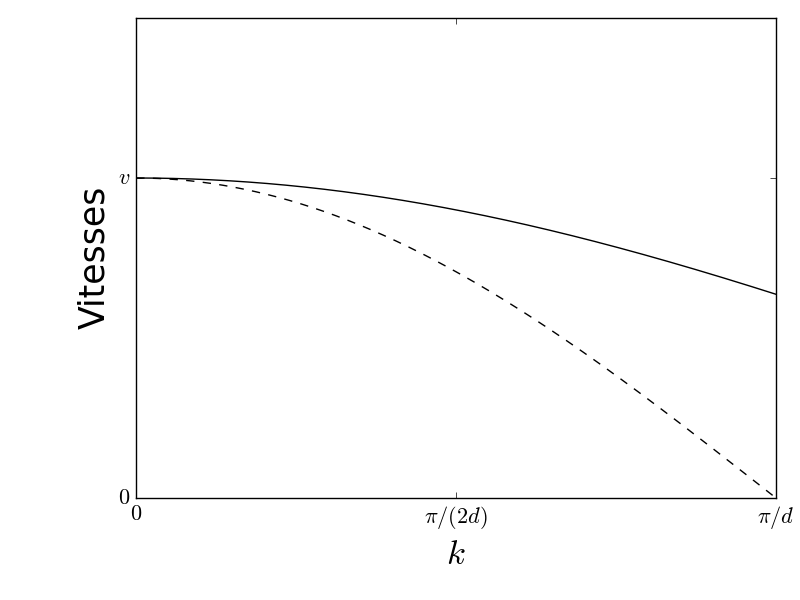
Les pulsations supérieures à ne sont pas atteintes, il s’agit d’un filtre passe-bas.