Magnétostatique
Exercice 22 ⭐️ Solénoïde épais, classique, Spé/L2
On considère un manchon cylindrique (un solénoïde “épais”) d’axe de rayon intérieur et de rayon extérieur , de longueur , constitué par l’enroulement de n spires en acier par unité de longueur, uniformément réparties sur le volume du cylindre. Le manchon peut être considéré comme infini : . Les spires sont parcourues par un courant variable . On se place dans l’ARQS.
À l’extérieur du manchon, le champ magnétique est le même que celui produit par un solénoïde “infini” possédant des spires de rayon . En déduire le champ magnétique en tout point de l’espace.
Réflexe
Détermination du champ en tout point de l’espace 👉 Théorème d’Ampère.
Corrigé
Pour , comme pour un solénoïde “fin”.
Les coordonnées adaptées à la symétrie du problème sont les coordonnées cylindriques. Soit un point de l’espace.
Direction de : Le plan contenant , perpendiculaire à est plan de symétrie de la distribution de courant, donc est perpendiculaire à ce plan, .
Paramètres d’espace de : il y a invariance du problème par translation prallèlement à , donc est indépendant de , et par rotation autour de , donc est indépendant de .
On utilise le théorème d’Ampère en choisissant un contour rectangulaire dont deux côtés sont parallèles à , de longueur selon l’axe , dont l’un des côtés parallèle à passe par M, et l’autre est extérieur au cylindre , l’autre côté qui lui est parallèle passant par . Ce contour est orienté pour que la normale soit selon le vecteur en .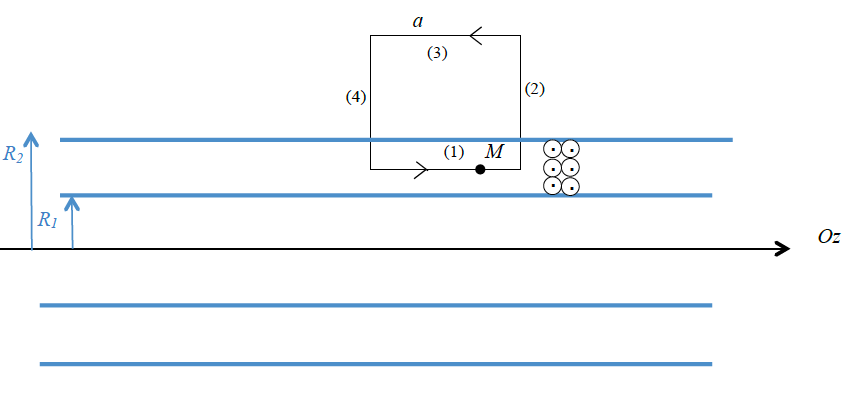
.
car , et sur . D’où
.
Exprimons le vecteur densité de courant entre et : homogène car en .
• pour , . D’où .
• pour . D’où . On retrouve évidemment le cas classique du solénoïde infini : à l’intérieur du solénoïde.
Le champ est une fonction continue de l’espace, comme attendu pour une distribution volumique.
Exercice 24 ⭐️⭐️⭐️⭐️ Tension de rupture d’un solénoïde, Spé/L2
X MP 2019.
Soit un solénoïde cylindrique de rayon et de longueur , de nombre de spires par unité de longueur . Le fil électrique qui constitue l’enroulement, non extensible, est caractérisé par une tension de rupture , au delà de laquelle le fil se casse.
- Montrer qu’il existe un courant maximal dans le solénoïde pour éviter la rupture. Le déterminer.
AN: cm, tours/mm, N.
Au vu des données, indiquer ce qui se passerait en réalité en injectant le courant calculé précédemment dans le solénoïde décrit par les données numériques. Comment y remédier ?
Que se serait-il passé avec un solénoïde fini? Où le fil a-t-il alors le plus de chance de céder (qualitativement) ?
Réflexe
Tension maximale 👉 Etablir le bilan des actions mécaniques exercées sur le solénoïde.
Indice
Modéliser le solénoïde par une distribution continue de courant, et déterminer la force de Laplace qui s’exerce sur un élément de longueur du solénoïde.
Corrigé
- Qualitativement, le solénoïde crèe un champ magnétique . Il y a donc une force de Laplace qui s’exerce sur un élément de fil du solénoïde . Un élément de fil entre et est en équilibre sous l’action des deux tensions, et exercées aux deux extrémités en et , et la force de Laplace.
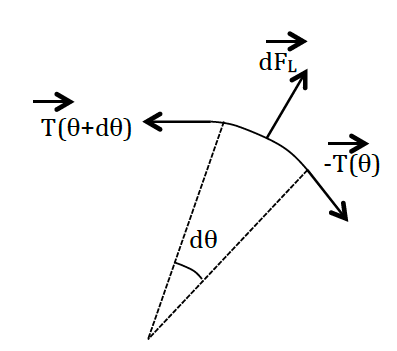
En projetant parallèlement à :
.
En projetant perpendiculairement à :
, soit , la tension est de norme constante .
De la première équation on tire .
La condition s’écrit donc . Reste à déterminer .
Dans le modèle du solénoïde infini, il y a une discontinuité du champ à la traversée du solénoïde. On peut considérer une distribution continue de courant entre et , on trouve à une distance r comprise entre et un champ , maximal en . Si on veut juste avoir un ordre de grandeur, on peut prendre (ou ), ce qui donne , soit
A.N. : .
Le courant très important va vraisemblablement conduire à ce que le fil constituant le solénoïde fonde sous l’action de l’échauffement créé par l’effet Joule (à moins que le fil ne soit en matériau supraconducteur, comme dans les “aimants” supraconducteurs. Dans ce cas, la résistance du bobinage est nulle et il n’y a pas d’effet Joule limitant la création de fort courant, et donc de champ magnétique intense. En revanche, le problème de la tension de rupture est à prendre en compte).
Avec un solénoïde fini, le même phénomène de rupture peut se produire. Il se produit en premier lieu là où le champ est le plus intense, donc au milieu du solénoïde.
Exercice 30 ⭐️⭐️ Distribution volumique de courant, Spé/L2
Une distribution volumique de courant est telle que
où est une constante. Déterminer le champ magnétique
- en un point de coordonnées cartésiennes .
- en tout point de l’espace.
Réflexes
Calcul du champ en tout point 👉 Théorème d’Ampère.
Corrigé
Le plan est plan de symétrie de la distribution de courant.
Le plan passant par et parallèle à est plan de symétrie de la distribution de courant.
Donc le champ doit être perpendiculaire à ces deux plans.Direction de . Le plan passant par et parallèle à est plan de symétrie de la distribution de courant. Donc .
Paramètres d’espace de . La distribution de courant est invariante par translation selon ou . D’où .
Théorème d’Ampère. Le plan étant plan de symétrie de la distribution de courant, . Déterminons pour , en appliquant le théorème d’Ampère à un contour rectangulaire parallèle à , de longueur selon l’axe dans le plan , l’autre côté qui lui est parallèle passant par . Ce contour est orienté pour que la normale soit selon le vecteur .
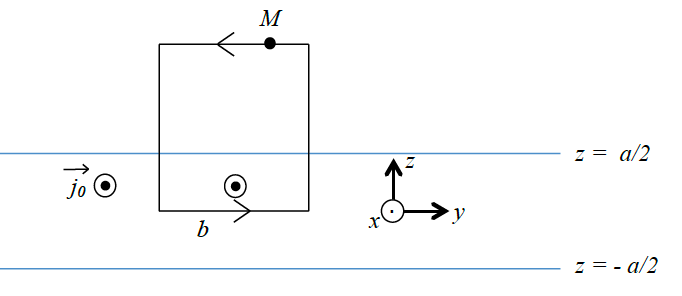
. L’intégrale est nulle pour les côtés verticaux du schéma et en . D’où : .
• Pour , et .
• Pour , et .
Finalement :
pour , .
pour , .
pour .
On retrouve à l’extérieur de la distribution le champ créé par une nappe de courant .
Exercice 50 ⭐️⭐️ Champ dans une cavité, Spé/L2/Classique
Un cylindre “infini”, de rayon , d’axe , est percé d’une cavité cylindrique infinie d’axe parallèle à , de rayon , telle que et . Le cylindre est parcouru (hormis la cavité) par une densité volumique de courant unifome . Déterminer le champ magnétique dans la cavité.
Corrigé
L’idée est d’utiliser le théorème de superposition : est la superposition du champ créé par un cylindre infini plein, de rayon , d’axe , parcouru par , et du champ créé par un cylindre infini plein, de rayon , d’axe , parcouru par .
• Déterminons .
Les coordonnées adaptées à la symétrie du problème sont les coordonnées cylindriques. Soit un point de l’espace, .
Direction de : le plan contenant et est plan de symétrie de la distribution de courant, donc est perpendiculaire à ce plan,
.
Paramètres d’espace de : il y a invariance du problème par translation prallèlement à , donc est indépendant de , et par rotation autour de , donc est indépendant de .
.
On utilise le théorème d’Ampère en choisissant un contour circulaire d’axe , passant par :
, soit
d’une part .
d’autre part pour qui est le seul cas utile ici , d’où
.
• Pour calculer la démarche est la même. Attention et n’ont pas la même signification.
• On réécrit les champs ,
.
D’où , soit :
Le champ est uniforme dans la cavité.