Filtrage, signaux
Exercice 119 ⭐️⭐️ Circuit à ALI, Mines Ponts PSI 2019, PSI/PT/L2
L’ALI du montage ci-dessous est idéal de gain infini et fonctionne en régime linéaire.
Faire une analyse qualitative du circuit à haute fréquence et à basse fréquence.
Exprimer la fonction de transfert. De quel type de circuit s’agit-il ?
Pour et pour . Exprimer .
Réflexe
ALI idéal en régime linéaire 👉 et .
Corrigé
En basse fréquence, le condensateur équivaut à un interrupteur ouvert. Comme , le courant dans et .
L’ALI est en régime linéaire donc . Donc le courant entre l’entrée et l’entrée - de l’ALI est nul. Comme , .
En haute fréquence, le condensateur équivaut à un fil : . Comme l’ALI est en régime linéaire . Le courant dans les deux résistances étant le même puisque , .Plaçons- nous en régime sinusoïdal forcé, en utilisant la représentation complexe.
La loi des nœuds donne à l’entrée -
La loi des nœuds donne à l’entrée +
:
D’où la fonction de transfert
, il s’agit d’un circuit déphaseur.L’équation différentielle reliant les tensions d’entrée et de sortie peut s’obtenir directement, ou simplement à partir de la fonction de transfert en identifiant la multiplication par à la dérivation par rapport au temps.
.
Pour ,
D’où avec .
Pour , le condensateur s’est déchargé, d’où . Par continuité de la tension aux bornes d’un condensateur , .
D’où le courant circulant dans les deux résistances est et . D’où
Exercice 137 ⭐️⭐️⭐️ Filtre de Wien, CCMP 2021, Spé/L2
- Prévoir qualitativement la nature du filtre suivant :
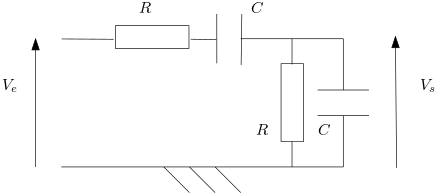
- Déterminer la fonction de transfert et tracer l’allure du diagramme de Bode.
- Le signal d’entrée est un un signal triangulaire de fréquence 100 kHz.
a. Est-il possible de choisir et pour obtenir une sinusoïde de fréquence 300 kHz ?
b. Est-il possible de choisir et pour obtenir un signal créneau de fréquence 100 kHz ?
Rappel : décomposition en série de Fourier d’un signal triangulaire pair d’amplitude maximale et de fréquence :
Réflexe
Signal sinusoïdal 👉 Par définition, un seul terme dans la décomposition de Fourier, il faut éliminer les autres !
Signal créneau/signal triangulaire 👉 L’un est la dérivée par rapport au temps de l’autre, à un facteur multiplicatif près.
Corrigé
- À hautes fréquences, les condensateurs équivalent à des fils. La tension de sortie, prise au bornes d’un condensateur, est nulle.
À basses fréquences, les condensateurs équivalent à des interrupteurs ouverts. Il n’y a pas de courant circulant dans le dipôle de sortie, la tension de sortie est nulle.
Il s’agit a priori d’un passe-bande. - Pour un signal d’entrée sinusoïdal, de pulsation , l’ensemble (R,C) en parallèle a une impédance telle que ,
Avec un diviseur de tension,
La fonction de transfert est bien celle d’un passe-bande du second ordre, de la forme avec , , . La fréquence de résonance est , la bande passante à -3 dB est .
Gain en dB et phase en fonction de .
3.a. Pour isoler l’harmonique 3 et ainsi obtenir un signal sinusoïdal de 300 kHz, il faut un filtre de fréquence de résonance pour sélectionner l’harmonique 3 du signal d’entrée. Idéalement, il faut un filtre très sélectif (de grand facteur de qualité), ce qui permet de supprimer les autres harmoniques et le fondamental. Dans le cas présent, le facteur de qualité est imposé égal à 1/3. Calculons les fréquences de coupure
.
.
Avec , il y a deux solutions positives (une pour +, une pour -)
, soit et .
Pour kHz, cela donnerait les fréquences de coupure et . et sont dans la bande passante, le signal de sortie ne sera pas sinusoïdal puisque le filtre laisse passer le fondamental et l’harmonique 5.
3.b. La dérivée d’un signal triangulaire est un signal créneau. Pour , la fonction de transfert , le filtre fonctionne en dérivateur (avec multiplication par ).
Il faut donc On peut prendre par exemple et pour obtenir un signal créneau en sortie.
Exercice 138 ⭐️⭐️ Circuit dérivateur, Spé/L2
- Dans quel domaine de fréquences le circuit ci-dessous présente-t-il un caractère dérivateur ? On donne et .

- On applique à l’entrée du circuit précédent une tension triangulaire d’amplitude 1V, de fréquence ou . On obtient les chronogrammes pour et pour . Cela vous semble-t-il cohérent (on admet que les coefficients du développement en série de Fourier d’une fonction triangle variant en , il suffit de prendre en compte les harmoniques )?
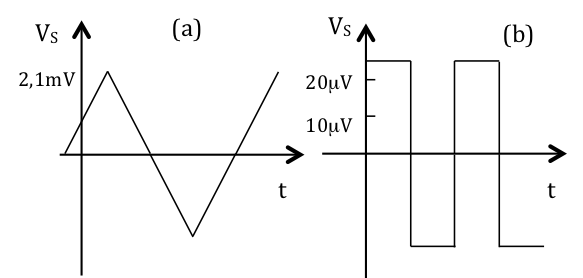
Réflexes
- Circuit dérivateur 👉 La fonction de transfert correspondante en régime sinusoïdal forcé est équivalente à réel.
- Modélisation d’un condensateur à “haute” (resp. “basse”) fréquence 👉 Fil (resp. interrupteur ouvert). Mais que signifie “haute” ou “basse” fréquence ?
Corrigé
Pour répondre, on se place en régime sinusoïdal forcé. On vérifie facilement que les très hautes fréquences (condensateur équivalent à un fil) ou très basses fréquences (condensateur équivalent à un interrupteur ouvert) ne permettent pas d’obtenir un dérivateur.
En remarquant , on peut se demander ce que signifie ici l’expression “haute fréquence” ou “basse fréquence” ? Il s’agit de comparer l’impédance du condensateur, de module , aux autres impédances présentes, ici et . On peut se trouver dans la situation , ce qui correspondrait à se trouver “à haute fréquence” relativement à , mais “à basse fréquence” relativement à .
Dans ce cas l’association en parallèle de et se comporte comme s’il y avait seulement le condensateur .
On a ainsi le condensateur et la résistance en série et
Remarque — Comme , on pourrait considérer que, dans l’association condensateur et résistance en série, le condensateur se comporte comme un interrupteur ouvert, mais alors le signal de sortie devrait être nul. On peut en déduire que l’amplitude du signal de sortie est a priori très faible devant l’amplitude du signal d’entrée.
On a bien un circuit dérivateur pour
soit
- correspond aux basses fréquences et . Le condensateur équivaut à un interrupteur ouvert et on a juste à cette fréquence et en série, soit un diviseur de tension avec .
Si on se limite aux premiers termes du développement en série de Fourier , chacun terme vérifie la condition (facteur 2 un peu juste pour …), et le signal triangulaire est transmis tel quel, avec une atténuation de . - , ainsi que les harmoniques 3 et 5 correspondent au domaine étudié au 1), Le circuit se comporte comme un dérivateur , ce qui justifie la forme créneau observée, dérivée du signal triangulaire.
Le facteur multiplicatif est très faible (voir remarque plus haut), et justifie l’amplitude du signal de sortie.
Exercice 139 ⭐️⭐️ Recherche d’un filtre, Spé/L2
On cherche à effectuer un filtrage passe-bas tel que:
- les pulsations inférieures à 1,5.10 rad.s doivent passer
sans être amplifiées et sans être atténuées de plus de 3 dB. - les pulsations supérieures à 4,0. 10 rad.s doivent
être atténuées d’au moins 15 dB.
Proposez un type de filtre qui puisse convenir, puis sa réalisation expérimentale.
Corrigé
Quand la pulsation passe de 1,5.10 rad.s à 4,0.10 rad.s, l’atténuation doit être au moins de 12 dB (on passe de -3 dB à -15 dB).
Considérons une variation du gain de la forme , alors est la pente par décade. La valeur absolue de la pente du gain en dB dans le diagramme de Bode doit donc être supérieure à .
Il ne peut donc s’agir d’un filtre d’ordre 1, dont la pente est de -20 dB par décade. En revanche un filtre d’ordre 2 peut convenir, avec une pente de -40 dB par décade.
Un exemple simple de passe-bas d’ordre 2 est un circuit série R, L, C, la tension de sortie étant prise aux bornes du condensateur. Alors, la fonction de transfert est de la forme normalisée
avec et le facteur de qualité .
Pour éviter une amplification comme demandé, il faut éviter la présence de résonance, donc .
En choisissant et , la condition 1) est bien vérifiée.
La condition 2) devrait l’être également. On vérifie en calculant pour et .
. La condition 2) est donc vérifiée.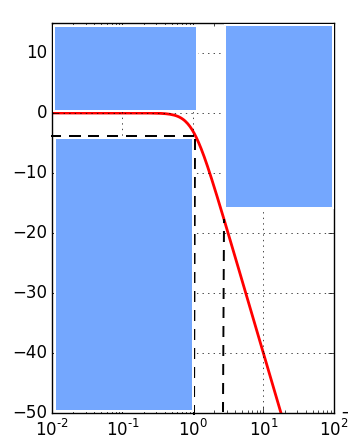
Gain en fonction de (en bleu les zones interdites par les contraintes imposées).